Arithmetic Progressions

Arithmetic Progressions

Definition:

By an arithmetic progression of m terms, we mean a finite sequence of the form

                        a, a + d, a + 2d, a + 3d, . . . , a + ( m - 1)d.

The real number a is called the first term of the arithmetic progression, and the real number d is called the difference of the arithmetic progression.

Example 1:

Consider the sequence of numbers

                                 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23.

This sequence has the property that the difference between successive terms is constant and equal to 2.

Here we have: a = 1; d = 2.

Example 2:

Consider the sequence of numbers

                                      2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32.

This sequence has the property that the difference between successive terms is constant and equal to 3.

Here we have: a = 2; d = 3.

General term of arithmetic progression:

The general term of an arithmetic progression with first term a₁ and common difference d is:

                                                  

Example 3: Find the general term for the arithmetic sequence -1, 3, 7, 11, . . . Then find a₁₂.

Solution:

Here a₁ = 1. To find d subtract any two adjacent terms: d = 7 - 3 = 4. The general term is:

                                               

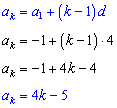
Video of Arithmetic Progressions:

Here are some exercise you may able to try with:

1.The third and eighth terms of an arithmetic progression are -5 and 15 respectively. Find
(a) The first term and the common difference
(b) The sum of the first 10 terms.

2.The first three terms of an arithmetic progression are 2k, 3k+3, 5k+1.Find
(a) the value of k,
(b the sum of the first 15 terms of the progression.

3.Given an arithmetic progression p+9, 2p+10, 7p-1,…., where p is a constant. Find
(a) the value of p,
(b) the sum of the next five terms.

Original Resource:

http://www.mathportal.org/algebra/progressions/arithmetic-progressions.php